Всегда - раньше или позже - наступает момент, когда вам захочется летать чуть-чуть быстрее. Может, вы побывали на соревнованиях и увидели, какую скорость показывают лучшие пилоты, причем при совершенно неблагоприятных погодных условиях. Кто-то из вас решил получить значок ФАИ, кому-то нужно просто пролететь больший маршрут в обычном тренировочном полете. Мы все привязаны к этому спорту жаждой постоянного совершенствования, и чуть-чуть большая путевая скорость оказывается в центре этого стремления.

Многие пилоты полагают, что путь к более скоростным полетам лежит через трату больших денег на новые современные планеры. Некоторые отказываются от участия в соревнованиях только потому, что "на этой старой штуковине не получится показать никаких результатов". В действительности же, маленькие различия в тактике пилотов полностью покрывают огромные преимущества дорогих стеклопластиков. Причина, по которой на вершине турнирных таблиц оказываются новейшие планера, заключается лишь в том, что лучшие пилоты готовы вкладывать все свои деньги и усилия для того, чтобы летать на лучших планерах. Но можно не сомневаться, что лучшие пилоты все равно будут первыми, даже летая на планерах двадцатилетней давности.

Чтобы увидеть результат, который может быть получен благодаря небольшим расчетам и размышлениям и последующей реализации их на практике, давайте поставим перед собой цель сократить количество выполняемых спиралей на три спирали в час. На самом деле это уже много: около одной дополнительной спирали в каждом потоке. А ведь сколько из нас, как минимум трижды в течение часа, выполняют спираль, которая не приносит никакого результата? То ли потому, что сам поток находится в другом месте, то ли потому, что мы не приняли вовремя решение пойти на переход, то ли потому, что плохо отцентрировали поток. Такая цель вполне может быть достигнута в тренировочных полетах в течение одного сезона.

Выполнение каждой спирали занимает около 25 секунд; трижды по 25 секунд - это 75 секунд, которые составляют в одном часе 2 % времени, что эквивалентно 20 соревновательным очкам. На рис. 1 я показал действительные гандикапы SSA, применяемые для соотношения качества и стоимости планера. На графике видно, что стоимость трех лишних спиралей за час - это около 10 000! Это равнозначно тому, чтобы, не неся дополнительных расходов, увеличить качество своего планера или вообще пересесть на планер следующего поколения. А, имея такой выбор, не лучше ли быть лучшим пилотом на более простом планере, чем быть плохим пилотом, но зато летать на дорогом планере?

Рис 1. Сколько стоит качество планера

Так как же начать быстрее летать? Я не стану утверждать, что летаю быстро, однако знаю тех, кто летает именно так. Я много наблюдал за быстрыми пилотами, слушал их рассказы, читал о них статьи и старался понять то, что они делают и о чем говорят. Кстати, они не всегда делали и говорили одни и те же вещи. Мне удалось усовершенствовать классическую теорию Мак-Креди, с учетом того, что потоки всегда являются случайными, а высота - ограниченной (См. "Mac Cready Theory with Uncertain Lift and Limited Altitude," Technical Soaring 23(3) (July 1999)88-96, также найти можно здесь). Эта математическая теория как будто очень хорошо подтверждается действиями пилотов. Однако техника и тактика со времен создания теории, описанной Моффатом, Райхманном, Биарами и Хольбруком, очень сильно изменились, поэтому я и хотел бы указать на некоторые новшества.

В каждый момент полета вам приходится принимать решения на основании некоторой "уверенности" или "агрессивности". Количественно степень вашей "уверенности" можно измерить путем ответа на вопрос: "сколько мне нужно еще набрать высоты, чтобы прилететь на финиш на одну минуту раньше?" Ответ на этот вопрос я назвал бы "числом Мак-Креди". Если число Мак-Креди равно 2, то это значит, что вы сможете финишировать на одну минуту раньше, если наберете дополнительно 120 метров высоты. Суть всей этой игры - выгодно "приобрести" высоту за счет увеличения общего времени и наоборот. Число Мак-Креди - это "цена" времени, выраженная в футах или метрах высоты.

Число Мак-Креди - это ключ в принятии любых решений в полетах на скорость. Очень просто: если число Мак-Креди равно 2, то вам следует останавливаться в любом потоке, превышающем по силе 2 м/с, и не тратить время в потоках, которые слабее этого значения. Если для того, чтобы финишировать на одну минуту раньше, необходимо набрать дополнительно 120 метров, то, очевидно, имеет смысл потратить эту же минуту, чтобы набрать дополнительно все 150 метров; но нет никакого смысла терять эту минуту, чтобы подняться всего на 90 метров.

Когда необходимо, это правило может также помочь определить, чему равно число Мак-Креди. Какая минимальная скороподъемность потока, при которой следует остановиться? Ответ на этот вопрос дает число Мак-Креди.

Число Мак-Креди дает возможность правильно определить скорость перехода по кольцевому калькулятору. Если вы "покупаете" высоту, скажем, 120 метров за одну минуту, то и тратить 120 метров высоты следует не быстрее, чем за одну минуту. Конечно, это не значит, что нужно лететь со скоростью, при которой снижение планера составит 120 метров в минуту. Это значит, что вам следует лететь со скоростью, при которой одна выигранная минута во времени полета будет стоить вам 120 метров. Около 50 лет назад Пол Мак-Креди показал, как можно вычислить эту скорость, и сегодня этот ответ запрограммирован в каждом бортовом компьютере и описан в любой книге о парящих полетах. Если вы увеличиваете скорость с 130 до 135 км/ч, летя на обычном планере, то каждая минута, на которую вы сокращаете время полета, будет дополнительно стоить около 60 метров высоты. Таким образом, если вы решили, что имеет смысл тратить 60 метров в минуту для достижения большей скорости, то и скорость в неподвижной атмосфере должна составлять 135 км/ч.

Все это хорошо, если число Мак-Креди известно. Однако какое именно число Мак-Креди окажется наиболее правильным? Какова на самом деле взаимная стоимость высоты и времени? Насколько агрессивными следует вам быть? Здесь мы уже выходим за пределы действия математической логики. Только многолетний опыт наблюдений за погодой и изучения находящихся впереди потоков может отличить профессионалов. Но все-таки мы можем найти правильные ответы для некоторых простых и типичных ситуаций, и эти ответы - достаточно полезный способ построить наше мышление так, чтобы практически определять значение Мак-Креди в полетах.

Мак-Креди

Если вы знаете скороподъемность следующего потока, а также уверены, что можете до него долететь, то это и будет числом Мак-Креди на переходе к этому потоку. Если вы знаете, что скороподъемность следующего потока - 2 м/с, то установите кольцевой калькулятор на 2 и выберите соответствующую скорость. Если по пути вам встретится поток со скороподъемностью 3 м/с, то в нем следует остановиться. И совершенно очевидно, что не стоит задерживаться где-либо, если скороподъемность потока будет менее 2 м/с.

Райхманн

Райхманн усовершенствовал эту теорию. Сила потока у его основания и на вершине уступает по значению силе потока в средней его части. Так что какую часть потока вы используете? Райхманн показал, что в качестве числа Мак-Креди на переходе следует использовать ожидаемую начальную скороподъемность следующего потока, которая должна быть равна скороподъемности предыдущего потока на вершине перед выходом из него. Если вы выберите несколько большую скорость, то вам придется восстанавливать высоту в более слабой части потока, а не в скороподъемной части потока ближе к его центру и вершине.

Безусловно, всегда следует использовать поток, если он окажется сильнее, чем текущее значение числа Мак-Креди. Райхманн применил эту концепцию при определении правила набора в потоках: оставайся в потоке до тех пор, пока набор в нем не уменьшится и не станет равным начальной скороподъемности в следующем потоке. Итак, правило Райхманна: начальный набор в следующем потоке = число Мак-Креди = набор в предыдущем потоке перед выходом. Райхманн также задумался о том факте, что нужно учитывать возможность долета до следующего потока. Число Мак-Креди следует уменьшать, если без этого вам придется совершить посадку до того, как вы доберетесь до следующего потока!

Концепция Райхманна очень важна, чтобы понять, как летают лучшие пилоты. Они летают намного медленнее, чем следовало бы согласно "классической" теорией Мак-Креди, которая основывается на использовании лучшей части потока. Неравномерность скороподъемности в одном и том же потоке по высоте, а также осознание того, что начальный набор в потоке часто происходит с меньшей скороподъемностью - это уже две весомые причины для того, чтобы уменьшить используемое число Мак-Креди.

Классический долет

Классический долет - еще один пример необходимости правильно рассчитать число Мак-Креди. Если вы находитесь на удалении 30:1 от финишной линии, и при этом впереди нет восходящих или нисходящих потоков, то установка кольцевого калькулятора на 2 для обычного стандартного 15-метрового планера приведет к полному расходованию высоты. В данной ситуации поток, поднявший вас на 120 метров выше, позволит вам лететь с большей скоростью и финишировать на одну минуту раньше. Если же вы встретите еще более сильный поток, то в нем также следует остановиться и финишировать еще быстрее.

Случайность потока и ограниченная высота

Все эти расчеты вполне наглядны, однако при этом заметно упрощены. Основная проблема заключается в том, что на самом деле вы не можете знать, где именно окажется следующий восходящий поток, также как и предугадать силу этого потока. Мы же хотим знать, каким будет число Мак-Креди в зависимости от вероятности нахождения потока той или иной силы.

На рис. 2 дан ответ и на этот вопрос - для полета на планере Discus в типичных условиях Восточного побережья. Высота потоков на вертикальной оси графика на рис. 2 может составлять от 500 до 1500 метров, на другой оси я указал вероятность нахождения потоков в соответствии с таблицей 1. Например, если рассматривать второй столбик таблицы, то вероятность встречи потока силой 0,5 м/с на протяжении одной мили составляет 20 %, вероятность встречи потока силой 1 м/с - 10 % и так далее. Иногда попадаются потоки силой 2 и 3 м/с, однако встречаются они настолько редко, что вам не следует рыскать туда-сюда в надежде встретить именно такой поток. Тем не менее, вы всегда должны стремиться к тому, чтобы выбранная вами стратегия полета позволяла максимально воспользоваться найденными потоками.

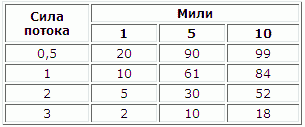
Таблица 1. Вероятность нахождения потока указанной силы (м/с) в зависимости от продолжительности перехода (в милях).

Рис. 2. Зависимость числа Мак-Креди от высоты полета для планера Discus в типичных условиях Восточного побережья (согласно Таблице 1)
Исходя графика на рис. 2, можно вывести несколько правил.

1. Уменьшайте число Мак-Креди по мере того, как вы теряете высоту - летите на меньшей скорости и останавливайтесь даже в более слабых потоках.

Число Мак-Креди увеличивается от 0-0,5 - на высоте 300 метров до почти 2 - на высоте 1500 метров. Объяснение простое: неравномерная скороподъемность потока по высоте. Если на высоте 300 метров вы не собираетесь останавливаться в потоках, если они слабее 2 м/с, то вам суждено вскоре стать выдающимся пилотом - по количеству посадок на площадки.

Все мы, конечно, это понимаем. Даже в самых ранних разъяснениях к теории Мак-Креди давался совет: если вы находитесь на высоте ниже 600 метров, останавливайтесь в любом встреченном потоке. Очевидно, что если вы на высоте ниже 600 метров останавливаетесь в любом потоке, а на высоте 2500 метров вы не станете останавливаться в потоке, слабее 3 м/с, то вам следует интерполировать эти значения в зависимости от вашей высоты в пределах данного диапазона высот - и ни в коем случае не устанавливать кольцевой калькулятор на 3, если ваша высота меньше 600.

2. Наоборот, вам следует уходить из слабых и искать более сильные потоки по мере увеличения высоты полета.

Во многих книгах и учебниках делается предостережение о том, что после выпаривания с малой высоты очень важно быстро изменить ваше мышление, направленное на то, чтобы выпарить, и не стремиться удержаться в метровом потоке вплоть до нижней кромки облаков. Как только вы поднялись выше 600 метров, в день с хорошей парящей погодой вам следует лететь дальше и попытаться найти более сильный поток.

Учитывая свойство некоторых потоков формироваться в виде пузырей и иметь сразу несколько не ярко выраженных центров, а также в связи с возможностью потери потока пилотом, применение графика на рис. 2 может привести к "ступенчатому" набору. Вы оказались на малой высоте и встретили полутораметровый поток. Вы его используете. Однако на высоте около 1000 метров вам пора начинать беспокоится. В соответствии с графиком на рис. 2 вам следует уйти в поисках более сильного потока. Вы можете встретить такой поток почти рядом с прежним местом набора (со мной это случается гораздо чаще, чем мне хотелось бы), или же, пролетев какое-то расстояние, можете найти поток скороподъемностью 2 м/с.

Конечно, существует вероятность, что вы такой поток и не встретите, однако в основе всех расчетов лежит концепция, что на высоте 1000 метров вероятность встретить нечто лучшее намного выше, чем быть вынужденным останавливаться в слабом потоке. И когда вы действительно встречаете более сильный поток, у вас появится высота, которую вы сможете потом выгодно использовать. Нижняя кромка облаков в некотором смысле - это худшее место, в котором вы можете оказаться. Если вы встретили поток скороподъемностью 4 м/с, но под самой кромкой - вы никак не сможете им воспользоваться!

3. Используемое число Мак-Креди существенно меньше, чем максимальная скороподъемность в лучшем потоке в данный день.

В моих расчетах максимальная скороподъемность потоков в течение дня - это 3 м/с. При этом число Мак-Креди никогда не превышает 2, а в течение полета оно преимущественно будет равно 1,5. Расчеты снова подтверждают то, что мы слышим от пилотов во всем мире: заниженное число Мак-Креди дает возможность увеличить среднюю путевую скорость, поскольку благодаря этому вы сможете пролететь большее расстояние.

Основной принцип, лежащий в основе расчетов для графика, изображенного на рис. 2.

4. Число Мак-Креди на переходе должно быть равно скороподъемности потока, в котором будет происходить следующий набор.

Если вы знаете, что впереди по маршруту нет хороших восходящих потоков, то нужно начинать беречь высоту прямо сейчас. Предположим, вы находитесь на высоте около 1000 метров. Заглядывая вперед на 5 миль, вы оцениваете вероятность встречи потока силой 2 м/с как 1:2. Однако вероятность того, что такой поток не будет найден, также равна 1:2, при этом вы снизитесь до 600 метров и будете надеяться уже хотя бы на метровый поток. В данный момент число Мак-Креди должно быть равно 1,5. Такой принцип мышления очень хорош при определении числа Мак-Креди, которое следует установить на кольцевом калькуляторе. Я пользовался этим же принципом, ставя перед компьютером задачу рассчитать правильное число Мак-Креди для долета в зависимости от соотношения имеющейся высоты и расстояния до финиша.

На рис. 3 наглядно показано, как можно увеличивать пройденную дистанцию, не летя при этом на слишком малой скорости. Пилот, полету которого соответствует нижняя кривая графика - это типичный пилот 60-х годов. Он знает, что впереди по линии пути он встретит поток силой 3м/с, и устанавливает кольцевой калькулятор 3. Он летит быстро, и он будет впереди всех, если действительно сможет найти трехметровый поток. Однако вполне вероятно, что ему придется сеть на площадку до того, как он встретит такой поток, или же, что еще более вероятно, он, потеряв высоту, затем потратит много времени, выбираясь в слабых потоках. Пилот, летящий по верхней кривой, устанавливает кольцевой калькулятор на 1. Летя медленнее, он пролетает большее расстояние, и таким образом увеличивает свои шансы встретить сильный поток. Но если он такой поток действительно встретит, то его скорость окажется чересчур малой для парящих условий дня.

Пилот, летящий по средней кривой, находит "золотую середину". Имея большую высоту, он летит быстро. Начиная переход с 2000 метров, он имеет достаточно шансов встретить 3-метровый или же хотя бы 2-метровый поток. Итак, он устанавливает кольцевой калькулятор на 3, как и быстрый пилот. Но по мере того, как он теряет высоту, вероятность нахождения сильного потока уменьшается, и поэтому пилот остановится и в более слабом потоке. Так он постепенно уменьшает используемое число Мак-Креди, снижает скорость и останавливается для набора в более слабом потоке. Таким образом, если средний пилот встретит сильный поток, то он окажется в выигрыше за счет большей скорости на переходе, как и быстрый пилот. Если же он такого потока не встретит, то он тоже максимально выиграет, благодаря возможности пройти большее расстояние, также как и "медленный" пилот.

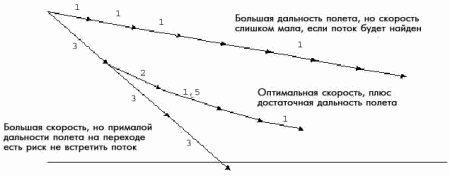
Рис. 3. Скорость и дальность полета на переходе

Кривая на графике, изображенном на рис. 2, не высечена на камне. На самом деле она может смещаться влево или вправо в зависимости от погоды, планера, а также от навыков и тактики самого пилота. Результаты любых расчетов зависят от исходных данных, и в случае изменения их значений, изменяется и результат.

Очевидно, кривая сдвинется влево в худших погодных условиях и вправо - в лучших. Также, хоть и не столь очевидно:
+ Форма кривой зависит от того, на какой высоте начинается рабочая часть потока. Если на меньшей высоте потоки слабые, то вскоре вы становитесь более осторожными и останавливаетесь для набора в более слабых потоках. Тенденция к снижению скороподъемности потоков на меньших высотах особенно часто наблюдается в ветреную погоду, в горах, в конце дня, а также когда скорость ветра изменяется по высотам.
+ Кривая зависит от высоты потоков и расстояния между ними. Чем больше расстояние между потоками, тем меньше должно быть число, установленное на кольцевом калькуляторе.
+ Один и тот же пилот в одних и тех же погодных условиях, летя на планере с меньшим качеством, должен выбирать более осторожную стратегию. Расчет такой же кривой для планера Schweitzer 1-26 показывает, что число Мак-Креди будет равно не 2, а 1,5. Это уже искусство - летать при качестве планера 1-26: вы вынуждены останавливаться в слабых потоках, чтобы не опуститься ниже критической высоты. Расчеты по классической теории Мак-Креди, которые предполагают, что любой пилот сможет долететь к одному и тому же потоку, умаляют преимущества планеров с более высоким качеством.
+ Менее опытный пилот должен лететь более осторожно, то есть кривая в его полете сдвигается влево. Если вы менее опытный по сравнению с другими пилотами, то вы сможете увеличить количество ваших очков, выбрав более осторожную стратегию полета, чем более опытные пилоты. Лучшие пилоты смогут найти поток, который вы и я пропустим. Поэтому мы во время полета должны оставлять себе больше шансов для того, чтобы получить в итоге лучший результат.
+ Опытные пилоты часто предлагают новичкам "просто лететь за ними и смотреть, что и как нужно делать". Это благородный совет, имеющий только благие намерения, если не вспоминать о том, какие длинные переходы совершают опытные пилоты, чтобы сбросить с хвоста своих соперников! Менее опытный пилот должен искренне поблагодарить и проигнорировать этот совет. (Если только этот опытный пилот действительно не собирается каждый раз задерживаться, чтобы вас подождать, и показывать, что и как делать. В этом случае нужно непременно воспользоваться этим редким и чрезвычайно полезным уроком!) Быстрый пилот всегда будет стартовать в самый последний момент. Стоит вам выполнить хотя бы пару лишних спиралей, и вы больше никогда этого пилота в этом полете не увидите, и вам придется добираться до своего аэродрома в одиночестве, в слабеющих к вечеру потоках. В худшем случае быстрый пилот, используя правильную для него тактику, может продолжать двигаться вперед на малой высоте, не имея под собой практически ни одной пригодной площадки. На самом же деле ведущий вас пилот может знать о том, что впереди есть поле, и у этого пилота есть достаточно опыта, чтобы до поля долететь и совершить на нем посадку. Вы же об этом поле не знаете, да и нет уверенности в том, что сможете благополучно посадить там планер. И если опытный пилот, наконец, встретит нужный поток, а вы нет, то тогда вы действительно окажетесь один на один с проблемой.
+ Правильная тактика зависит от того, как вы оцениваете взаимозависимость между увеличением скорости и возрастанием риска совершить преждевременную посадку. Если вы хотите уменьшить вероятность посадки на площадку, то всегда устанавливайте на кольцевом калькуляторе число 0. Но при этом вы действительно будете лететь слишком медленно. Чтобы лететь быстрее, вам просто придется смириться с большей вероятностью посадки на площадку. Для рис. 2 я рассчитывал сумму очков в случае посадки на площадку согласно правилам подсчета дистанционных очков на соревнованиях в США. Если на соревнованиях за пройденную дистанцию насчитывается больше очков, то следует выбирать более агрессивную тактику полета. Если ваше личное нежелание оказаться на площадке имеет для вас большее значение, чем возможность получить больше очков, то лететь следует более осторожно, особенно если вы оказались на небольшой высоте.

Все вышесказанное представляет собой общую концепцию того, как начать летать быстрее с учетом случайности потоков и необходимости иметь достаточную высоту для их поиска. Мы же должны задуматься еще над тем, что для центрирования потоков также требуется время. Уменьшение времени, затрачиваемого на центрирование потоков, - одна из самых важных составляющих в стратегии скоростных полетов, которая существенно влияет на среднюю путевую скорость. В следующей главе я начну с рассуждений именно по этому вопросу. Кроме того, мы поговорим о скорости перехода, отклонениях от линии пути, а также о долете.

Источник: http://gliding.com.ua